Alan ha tomado cursos de Ajedrez las últimas vacaciones invernales, y en los recreos ha estado jugando con sus amigos algunas partidas rápidas; Su compañero Diego está furioso porque nunca ha podido ganarle. Diego ha escuchado del profe de Computación un peculiar Ajedrez extendido en el que las fichas atraviesan los límites del tablero y continúan su movimiento en el borde opuesto. En sus típicos arranques de furia, Diego ha retado a Alan a resolver un problema en el Tablero extendido: Si ponemos en el tablero un Caballo en la posición (f,c), y a partir de esta posición el Caballo comienza a moverse en una de las ocho posibles variantes: Arriba Izquierda (AI), Arriba Derecha (AD), Abajo Izquierda (BI), Abajo Derecha (BD), Derecha Arriba (DA), Derecha Abajo (DB), Izquierda Arriba (IA), Izquierda abajo (IB). En su trayecto el Caballo es posible que alcance una casilla en la que estuvo antes. ¿Cuál es el mínimo número de movidas que el caballo puede realizar hasta alcanzar una casilla en la que ya estuvo?
Diego se ha memorizado las posibilidades para cada posición del caballo y está seguro de ganar contra Alan. Conociendo que Diego propone el reto, Alan pide que el tablero extendido pueda variar en tamaño. El tablero puede ser de NF x NC donde NF es el número de filas y NC es el número de columnas. El Caballo podrá moverse en la dirección escogida df casillas en las filas y dc casillas en las columnas. Así ambos tendrán que calcular la respuesta sin ventajas. El tablero se enumera desde la casilla superior izquierda; las filas hacia abajo y las columnas hacia la derecha.
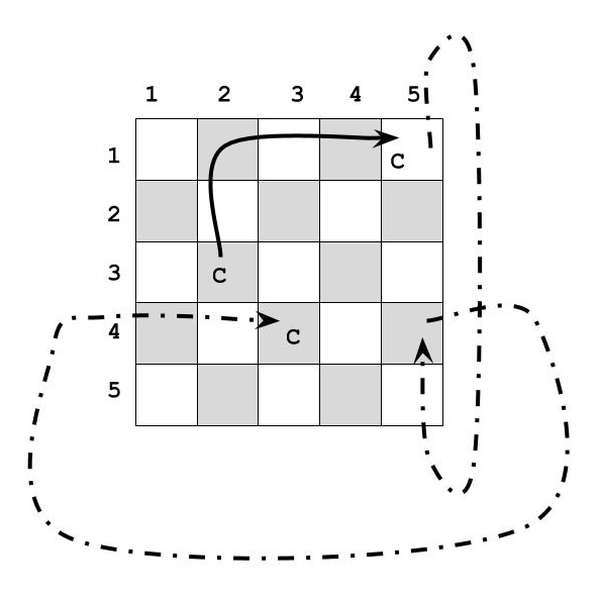
Por ejemplo, si se tiene un tablero de 5x5, y el caballo se halla en la posición (3,2) con desplazamientos en filas y columnas df = 2 y dc = 3; si el caballo se mueve AD acabará en la casilla (1,5), como ya no le es posible cambiar de dirección, continuará moviendo AD, luego a partir de (1,5) alcanzará la casilla (4,3).
Diego está desesperado y sabe que Alan es muy bueno calculando. Ayuda a Diego a conseguir un programa que calcule rápidamente los resultados y así pueda ganar el reto. ¡Diego no sabe programar, depende de ti!
La primera línea contiene un número M entero que indica la cantidad de casos de prueba. A partir de la segunda línea se tienen los casos de prueba (uno por línea), para cada caso de prueba se tiene seis números enteros positivos NF, NC, F, C, DF, DC y DIR. Donde NF y NC (1 ≤ NF, NC ≤ 10000000) representan el número de filas y columnas del tablero respectivamente; F y C (1 ≤ F ≤ NF y 1 ≤ C ≤ NC) es la posición inicial del caballo en fila y columna respectivamente; con DF y DC (1 ≤ DF < NF y 1 ≤ DC < NC ) el desplazamiento en fila y columna que el caballo debe realizar, DIR es la dirección que el Caballo seguirá (AI, AD, BI, BD, DA, DB, IA, IB).
Para cada caso de prueba imprimir la respuesta que consiste en el mínimo número de movidas que el caballo puede realizar hasta alcanzar una casilla en la que ya estuvo.
2 5 5 3 2 2 3 AI 6 5 2 2 1 5 DB
5 6
#obi-final-nacional #2017